【答案】

　　本题中，由于甲、乙两人在正常道路和泥泞道路上的速度都相同，可以发现，如果甲、乙各自绕着圆形跑道跑一圈，两人在正常道路和泥泞道路上所用的时间分别相同，那么两人所用的总时间也就相同，所以，两人同时出发，跑一圈后同时回到 A点，即两人在 A点迎面相遇，然后再从 A点出发背向而行，可以发现，两人的行程是周期性的，且以一圈为周期．

　　在第一个周期内，两人同时出发背行而行，所以在回到出发点前肯定有一次迎面相遇，这是两人第一次迎面相遇，然后回到出发点是第二次迎面相遇；然后再出发，又在同一个相遇点第三次相遇，再回到出发点是第四次相遇……可见奇数次相遇点都是途中相遇的地点，偶数次相遇点都是 点．本题要求的是第99次迎面相遇的地点与 点的距离，实际上要求的是第一次相遇点与 点的距离．

　　对于第一次相遇点的位置，需要分段进行考虑：由于在正常道路上的速度较快，所以甲从出发到跑完正常道路时，乙才跑了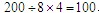 米，此时两人相距100米，且之间全是泥泞道路，此时两人速度相同，所以再各跑50米可以相遇．所以第一次相遇时乙跑了 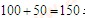米，这就是第一次相遇点与 点的距离，也是第99次迎面相遇的地点与 点的距离．

　　【答案】 150米