·每道题的答题时间不应超过15分钟。答案明日公布！

　　难度：★★★★

　　小学六年级奥数天天练：

　　兄弟二人三年后的年龄和是26岁，弟弟今年的年龄恰好是兄弟二人年龄差的2倍．问，3年后兄弟二人各几岁？

　　【答案】

　　分析 设3年后哥哥年龄为x岁，弟弟年龄为（26-x）岁．则今年哥哥年龄为（x-3）岁，弟弟年龄为（26-x-3）岁，兄弟二人的年龄差是（x-3）-（26-x-3）岁．列方程的等量关系是：弟弟今年的年龄=兄弟二人年龄差的2倍．

　　解：设3年后哥哥x岁，则弟弟3年后的年龄是（26-x）岁．

　　［（x-3）-（26-x-3）］×2＝26-x-3

　　［2x-26］×2＝23-x

　　4x-52=23-x

　　5x＝75

　　x＝15

　　26-x＝26-15＝11

　　答：3年后哥哥年龄是15岁，弟弟11岁．



　　难度：★★★★★

　　小学六年级奥数天天练：

　　在一个6×6的方格表中，任选5个方格涂黑，然后再逐步将凡是与两个或两个以上黑格相邻的方格涂黑，不断按这个法则做下去，证明：无论怎样选择最初的5个方格，都不可能按这样的法则将所有方格全部涂黑．

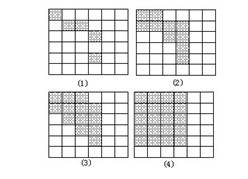
　　【答案】

　　先试验一下，在上图的方格表中选5格涂黑，然后按给定法则涂黑另一些格，直到上图（4），已无法再将其余的方格涂黑．如果改变最初5格的位置，虽然最后涂黑的部分会不同，但都不能将所有方格全部涂黑．为了证明这一结论，如果将最初5格的不同位置一一列举出来，再逐个证明，当然也是可以的（这种方法叫枚举法），不过过于繁琐．因此，应该在试验中寻求规律，不被表面现象迷惑．

　　证明：考虑涂黑过程中黑色区域的周界总长度．设小方格的边长为1，则开始有5个黑格，黑色区域总长度不大于20．按照题设的涂黑法则，每格在涂黑前后，黑色区域的周界不会变长（此方格至少有两边是原来黑色区域的周界，当此格涂黑后，这两边已不再是边界，而另两边可能成为边界）．如果能将所有方格都涂黑，那么黑色边界的总长度应为24，由以上分析，这是不可能的，因此，无论怎样选择最初的5个方格，都不可能按照题设的法则将全部方格涂黑．