学而思奥数天天练栏目每日精选中等、高等难度试题各一道。中难度试题适合一些有过思维基础训练、考 题学习经历，并且奥数成绩中上的学生。高难度试题立足于杯赛真题、综合应用和加深各知识点，适合一些志在竞赛中 夺取佳绩的学生。
·本周试题由学而思奥数名师刘斌精选、解析，以保证试题质量。
·每周末，我们将一周试题汇总为word版本试卷，您可下载打印或在线阅读。
·每道题的答题时间不应超过15分钟。答案明日公布！
难度：★★★★
【答案】
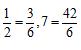，在4，5，…，41这38个数中，有19个是2的倍数，12个是3的倍数，6个6的倍数，因此其中有38-19-12+6=13 个与6互质，即答案为13．
难度：★★★★★
(第四届走美初赛试题)2006盏亮着的电灯，各有一个拉线开关控制，按顺序编号为l，2，…，2006.将编号为2的倍数的灯的拉线各拉一下；再将编号为3的倍数的灯的拉线各拉一下，最后将编号为5的倍数的灯的拉线各拉一下．拉完后亮着的灯数为__________盏．
【答案】
因为灯在开始的时候是亮着的，所以拉了两次或者没拉的灯最后还是亮的．这道题实际上是求 1到2006中不能被2、3、5整除的数和只能同时被2、3、5中2个数整除的数的总个数．
我们可以求得被2整除的数有 2006÷2=1003(盏)，
被3整除的数有 2006÷3=668L2，共668(盏)，
被5整除的数有2006÷5=401L1 ，共401(盏)．
其中，同时被2、3整除的数有2006÷（2×3）=334L2 ，共334(盏)；
同时被3、5整除的有2006÷（3×5）=133L11 ，共133(盏)；
同时被2、5整除的数有2006÷（2×5）=200L6 ，共200(盏)；
同时被2、3、5整除的数有2006÷（2×3×5）=66L26 ，共66(盏)，所以，只能同时被2、3、5中2个数整除的数的个数为 334+133+200-3×66=469(盏)，不能被2、3、5整除的数的个数为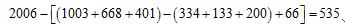 
(盏)．所以，最后亮着的灯一共为469+535=1004 (盏)．
名师介绍：
刘斌老师刘 斌老师教学最大特点是——系统，理性，亲和。从小学习奥数，并在全国重要杯赛中屡次获奖。从事奥数教育工作以来，注重学生的奥数知识体系掌握以及思维训 练，强调数学模型，引导学生一题多解和多题一解。帮助学生深刻理解数学思想，熟练掌握数学方法，灵活运用解题技巧。刘老师的课堂轻松活泼，富有亲和力和感 染力，节奏感强；学生与老师之间充分交流，使学生成为真正的课堂主体。
