奥数天天练栏目每日精选中等、高等难度试题各一道。中难度试题适合一些有过思维基础训练、考 题学习经历，并且奥数成绩中上的学生。高难度试题立足于杯赛真题、综合应用和加深各知识点，适合一些志在竞赛中 夺取佳绩的学生。
·本周试题由学而思奥数名师精选、解析，以保证试题质量。
·每周末，我们将一周试题汇总为word版本试卷，您可下载打印或在线阅读。
牛吃草问题
难度：★★★★
一块牧场长满了草，每天均匀生长。这块牧场的草可供10头牛吃40天，供15头牛吃20天。可供25头牛吃多少天？
【答案】
假设1头牛1天吃草的量为1份
（1）每天新生的草量为：(10×40-15×20)÷（40-20）=5（份）；
（2）原来的草量为：10×40-40×5=200（份）；
（3）安排5头牛专门吃每天新长出来的草，这块牧场可供25头牛吃：200÷（25-5）=10（天）。
难度：★★★★★
某游乐场在开门前已经有100个人排队等待，开门后每分钟来的游人数是相同的，一个入口处每分钟可以放入10名游客，如果开放2个入口20分钟后就没有人排队，现在开放8个入口处，每分钟关闭一个门，那么开门后几分钟就没人排队了？
【答案】
（1）每分钟来的游人数是：（20×10×2-100）÷20=15（名）游客
（2）第1分钟期间开了8个门，所以放入80名游客，还剩：100+15-80=35（名）游客
（3）第2分钟期间开7个门：由于70大于35+15=50，所以肯定是在第2分钟期间的某个时间就没人排队了，不妨设从第2分钟开始t分钟后就没人排队了，故t分钟内新来了15t个游客，7个门放入了7×10t个游客，所以由方程15t+35=7×10t，解得t=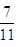
，即在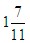
分钟后就没人排队了。
