小学六年级奥数题及答案:一半模型
1.一个正方形地板砖示意图,在大正方形ABCD中AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?
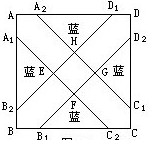
连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在DPC处(如图18和图19)。
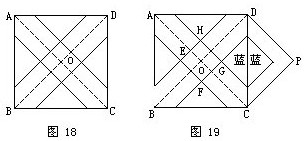
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。由此得出,正方形OCPD的边长是4+6=10厘米,当然正方形OCPD的面积就是102,即100平方厘米。而正方形OCPD的面积恰好是正方形ABCD的面积的一半,因此正方形ABCD的面积是200平方厘米。
答:正方形ABCD的面积是200平方厘米。
2.直线型面积
如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH。如果ABCD的面积是5平方厘米,则EFGH的面积是多少?
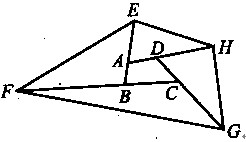
解答:不规则四边形的面积我们很难处理,不如把它切割成两个三角形。
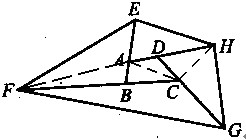
首先,连接AC,可以得到
S△BEF=3S△ABF=9S△ABC
S△DHG=3S△CDH=9S△ACD
因此,S△BEF+S△DHG=9(S△ABC+S△ACD)=9 S四边形ABCD
同样地,如果连接BD,可以知道S△AEH+S△CFG=9 S四边形ABCD
这样整个图形的面积为
S四边形EFGH=(9+9+1)S四边形ABCD=19×5=95(平方厘米)




