学而思奥数天天练栏目每日精选中等、高等难度试题各一道。中难度试题适合一些有过思维基础训练、考题学习经历，并且奥数成绩中上的学生。高难度试题立足于杯赛真题、综合应用和加深各知识点，适合一些志在竞赛中夺取佳绩的学生。

　　·本周试题由学而思教研部《小学奥数系统总复习》编者刘洋洋老师精选、解析，以保证试题质量。

　　·每周末，我们将一周试题汇总为word版本试卷，您可下载打印或在线阅读。

　　·每道题的答题时间不应超过15分钟。答案明日公布！

    【行程专题】

　　1．难度：★★★

　　A、B两地相距2400米，甲从A地、乙从B地同时出发，在A、B间往返长跑。甲每分钟跑300米，乙每分钟跑240米，在30分钟后停止运动。甲、乙两人在第几次相遇时A地最近？最近距离是多少米？

　　【解析】30×(300+240)÷2400=6.75个全程，相遇3次，把全程分成9份，第一次相遇，甲跑5份，第二次相遇甲跑15份，距离A3份，第三次相遇甲跑25份距离A7份，所以第二次相遇距离A最近，最近为2400÷9×3=800米。

　　2．难度：★★★

　　如图8，甲、乙两艘快船不断往返于A、B两港之间。若甲、乙同时从A港出发，它们能否同时到达下列地点？若能，请推出它们何时到达该地点；若不能，请说明理由：

　　（1）A港口；

　　（2）B港口；

　　（3）在两港口之间且距离B港30千米的大桥。

　　【解析】    （1）甲往返一次的时间是

　　，

　　乙往返一次的时间是

　　，

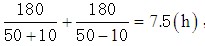　　13.5和7.5的最小公倍数是67.5，

　　所以，在甲、乙出发后的67.5a(a=1,2,……) 小时，它们又同时回到 A港。  （5分）

　　（2）设甲、乙能同时到达B 港，此时，甲、乙各完成了m,n 次往返（m,n 是自然数），则有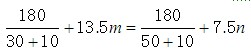

　　即   9m+1=5n      。

　　当 m的个位数是6或1时，有满足上式的自然数n 。最小的=1,最少需要4.5+13.5=18小时。则在甲、乙出发后18+67.5小时，它们同时到达港口。（10分）

　　（3）设甲、乙能同时到达大桥，且分别完成了m,n 次往返（ m,n是自然数）。

　　①若此时甲、乙向下游行驶，则

　　，

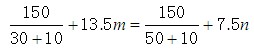　　即   135m+12.5=75n       ，

　　没有满足上式的自然数 m,n。

　　②若此时甲、乙向上游行驶，则

　　，

　　即 135m+22.5=75n  ，

　　没有满足上式的自然数m,n。

　　③若此时甲向上游行驶，乙向下游行驶，则

  

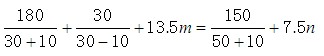
　　即27m+7=15n 

　　没有满足上式的自然数m,n 。

　　④若此时甲向下游行驶，乙向上游行驶，则

  

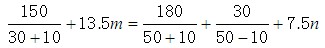
　　即9m=5n

　　当 m的个位数是0或5时，有满足上式的自然数 n，所以在甲、乙出发后的

   

　　小时，它们同时到达大桥。

　　（3）
 

-------------------------------------------------------------------------------------

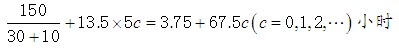
《小学奥数系统总复习》 图书简介

《小学奥数系统总复习》分 上下两册，涵盖了奥数中8大专题，共设21讲。每讲设置4大模块，即闯关目标、赛前热身、实战演练和逐级闯关，构建了完整的奥数知识体系，全面覆盖小学奥 数知识。此外，本书对部分经典例题录制了视频，免费赠送给各位学员。本书附有2010年和2011年的北京集训队选拔试题，为本书增加了新的亮点。     为了让大家更好的获得知识、理解知识，本书设有论坛交流环节，读者可以登录E度论坛点击进入图书答疑帖，即可实现在线提问、交流心得，名师天天坐镇论坛，等你来交流！